Determining the sample size in a clinical trial
Adrienne Kirby, Val Gebski and Anthony C Keech
MJA 2002 177 (5): 256-257

Abstract —
Introduction —
Components of sample size calculation —
Effect of compliance —
Allocation ratio —
Reporting the sample size section of the protocol —
Conclusion —
Acknowledgements —
References —
Author details


Sample size must be planned carefully to ensure that the research time, patient effort and support costs invested in any clinical trial are not wasted. Item 7 of the CONSORT statement relates to the sample size and stopping rules of studies (see Box 1); it states that the choice of sample size needs to be justified.1
Ideally, clinical trials should be large enough to detect reliably the smallest possible differences in the primary outcome with treatment that are considered clinically worthwhile. It is not uncommon for studies to be underpowered, failing to detect even large treatment effects because of inadequate sample size.2 Also, it may be considered unethical to recruit patients into a study that does not have a large enough sample size for the trial to deliver meaningful information on the tested intervention.
Components of sample size calculation
The minimum information needed to calculate sample size for a randomised controlled trial in which a specific event is being counted includes the power, the level of significance, the underlying event rate in the population under investigation and the size of the treatment effect sought. The calculated sample size should then be adjusted for other factors, including expected compliance rates and, less commonly, an unequal allocation ratio.
Power: The power of a study is its ability to detect a true difference in outcome between the standard or control arm and the intervention arm. This is usually chosen to be 80%. By definition, a study power set at 80% accepts a likelihood of one in five (that is, 20%) of missing such a real difference. Thus, the power for large trials is occasionally set at 90% to reduce to 10% the possibility of a so-called "false-negative" result.
Level of significance: The chosen level of significance sets the likelihood of detecting a treatment effect when no effect exists (leading to a so-called "false-positive" result) and defines the threshold "P value". Results with a P value above the threshold lead to the conclusion that an observed difference may be due to chance alone, while those with a P value below the threshold lead to rejecting chance and concluding that the intervention has a real effect. The level of significance is most commonly set at 5% (that is, P = 0.05) or 1% (P = 0.01). This means the investigator is prepared to accept a 5% (or 1%) chance of erroneously reporting a significant effect.
Underlying population event rate: Unlike the statistical power and level of significance, which are generally chosen by convention, the underlying expected event rate (in the standard or control group) must be established by other means, usually from previous studies, including observational cohorts. These often provide the best information available, but may overestimate event rates, as they can be from a different time or place, and thus subject to changing and differing background practices. Additionally, trial participants are often "healthy volunteers", or at least people with stable conditions without other comorbidities, which may further erode the study event rate compared with observed rates in the population. Great care is required in specifying the event rate and, even then, during ongoing trials it is wise to have allowed for sample size adjustment, which may become necessary if the overall event rate proves to be unexpectedly low.
Size of treatment effect: The effect of treatment in a trial can be expressed as an absolute difference. That is, the difference between the rate of the event in the control group and the rate in the intervention group, or as a relative reduction, that is, the proportional change in the event rate with treatment. If the rate in the control group is 6.3% and the rate in the intervention arm is 4.2%, the absolute difference is 2.1%; the relative reduction with intervention is 2.1%/6.3%, or 33%.
Estimating the plausible effect of treatment to be sought in a randomised controlled trial provides a further challenge, and may be the most common problem for reported trials. Too frequently, studies are designed to identify an implausibly large treatment effect (for example, a 30% to 50% reduction), when most important treatments that have been adopted into clinical practice have shown more modest benefits. When studies are designed to find unrealistically large reductions and fail, smaller real reductions are inevitably rendered statistically non-significant, leading to confusion about the value of the intervention studied. To resolve uncertainty, the study then needs to be repeated elsewhere, but with a larger sample size than before. Wherever possible, the minimum worthwhile difference in response should be determined from phase II or pilot studies and expert opinion from colleagues. Investigators should take into consideration any cost or logistical advantages or disadvantages of the interventional treatment compared with standard care.
From these components, sample size can be calculated as shown in Box 2. It can be seen that the required sample size increases as the chosen significance level becomes smaller and as the chosen power increases. Also, even a small change in the expected absolute difference with treatment has a major effect on the estimated sample size, as the sample size is inversely proportional to the square of the difference. Thus, if 1000 participants per treatment group are required to detect an absolute difference of 4.8%, 4000 per treatment group would be required to detect a 2.4% difference. Precise calculation of sample size for different types of outcomes (continuous, binary and time-to-event) is discussed in standard texts.3-5 A checklist for determining sample size is given in Box 3.
Effect of compliance
A major limitation of many sample size calculations is the failure to account for patients' predictable lack of compliance with their allocated treatments. As compliance losses directly affect the size of the achievable treatment difference, they also affect the estimated sample size in a non-linear fashion. For example, a placebo-controlled study needing 100 patients per treatment arm, with 100% compliance, would require about 280 patients per arm if compliance is only 80% in each group (that is, 20% of patients allocated the investigational treatment fail to take it, and 20% of patients allocated to the placebo-control arm cross over to the investigational treatment). The compliance adjustment formula is adjusted n per arm equals N/([c1+c2–1]2), where c1 and c2 are the average compliance rates per arm (so, in the above example, adjusted n = 100/([0.8+0.8–1]2) = 280).
Allocation ratio
A one-to-one allocation to intervention and control treatment arms is the most common form of random allocation and results in the smallest sample size requirement. Sometimes different allocation ratios are chosen, resulting in a larger total sample size needed to achieve the same power. This may be justified where the investigational treatment is unusually expensive or complicated to administer.
Reporting the sample size section of the protocol
The sample size calculation should be described in sufficient detail to allow its use in other protocols. The power, level of significance and the control and intervention event rates should be clearly documented. Information on the scheduled duration of the study, any adjustment for non-compliance and any other issues that formed the basis of the sample size calculation should be included. For continuous outcomes, in particular (eg, blood pressure), assumptions made about the distribution or variability of the outcome should be explicitly stated.
Conclusion
Estimating sample size is important in the design of clinical trials, and the quality of the estimate ultimately depends on the quality of the information used to derive it. Care should be taken to avoid overestimating the likely event rate and the feasible effects of treatment. The objectives and outcome measures of the study must be clearly stated,6 and the information used in calculating the sample size should reflect as closely as possible the type of data that will be gathered from the trial in question. Professional advice should be sought before embarking on any major trial project.

1: CONSORT checklist of items to include when reporting a trial1
Selection and topic
Item no.
Description
Methods Sample size
7
How sample size was determined and, when applicable, explanation of any interim analyses and stopping rules

2: Generic expression for calculating sample size
Sample size α
(power, inverse function of significance level*)
(absolute difference)2
* As the P value becomes smaller, the function of the significance level increases.

3: Checklist for determining sample size for clinical trials
Estimate the event rate in the control group by extrapolating from a population similar to the population expected in the trial.
Determine, for the primary outcome, the smallest difference that will be of clinical importance.
Determine the clinically justifiable power for the particular trial.
Determine the significance level or probability of a "false positive" result that is scientifically acceptable.
Adjust the calculated sample size for the expected level of non-compliance with treatment.

more



Statistical considerations for clinical trialsand scientific experiments
Find sample size, power or the minimal detectable difference for parallel studies, crossover studies, or studies to find associations between variables, where the dependent variable is Success or Failure, a Quantitative Measurement, or a time to an event such as a survival time.
Find:
Study Type
Measurement Type
Parallel study:
Success or Failure
Quantitative Measurement (JS*)
Time to an Event
Crossover study:
Quantitative Measurement (JS*)
Study to find an association:
Quantitative Measurement (JS*)
* — The JavaScript versions of these tools are currently in testing, and may not give the correct values. They are linked here for ease of access. Please do not rely on these tools at this time
This site was last updated on March 7th 2007. This update regularized the HTML, and added links to the test versions of the JavaScript based Quantitative Measurement tools
These calculations are based on assumptions which may not be true for the clinical trial you are planning. We do not guarantee the accuracy of these calculations or their suitability for your trial. We suggest that you speak to a biostatistical consultant when planning a clinical trial. Please contact us if you have any questions or problems using this software.
The author of these tools is David A. Schoenfeld, Ph.D. (dschoenfeld@partners.org), with support from the Massachusetts General Hospital Mallinckrodt General Clinical Research Center, Research Resources Division, National Institutes of Health, General Clinical Research Center Program.
Definitions
Sample size:
The number of patients or experimental units required for the trial.
Power:
The probability that a clinical trial will have a significant(positive) result, that is have a p-value of less than the specified significance level(usually 5%). This probability is computed under the assumption that the treatment difference or strength of association equals the minimal detectable difference.
Minimal detectable difference:
The smallest difference between the treatments or strength of association that you wish to be able to detect. In clinical trials this is the smallest difference that you believe would be clinically important and biologically plausible. In a study of association it is the smallest change in the dependent(outcome variable, response), per unit change in the independent(input variable, covariate) that is plausible.
Parallel design:
A parallel designed clinical trial compares the results of a treatment on two separate groups of patients. The sample size calculated for a parallel design can be used for any study where two groups are being compared.
Crossover study:
A crossover study compares the results of a two treatment on the same group of patients. The sample size calculated for a crossover study can also be used for a study that compares the value of a variable after treatment with it's value before treatment. The standard deviation of the outcome variable is expressed as either the within patient standard deviation or the standard deviation of the difference. The former is the standard deviation of repeated observations in the same individual and the latter is the standard deviation of the difference between two measurements in the same individual.
Study to find an association:
A study to find an association determines if a variable, the dependent variable, is affected by another, the independent variable. For instance, a study to determine whether blood pressure is affected by salt intake.
Success/Failure:
The outcome of the study is a variable with two values, usually treatment success or treatment failure.
Measurement:
The outcome of the study is a continuous measurement.
Time to an Event:
The outcome of the study is a time, such as the time to death, or relapse. Some patients will not have been observed to relapse. These observations are said to be censored.


more





Sample Size Calculations in Clinical Research
Shein-Chung ChowJun ShaoHansheng Wang
Read it Online!

Sample size calculation is usually conducted through a pre-study power analysis. The purpose is to select a sample size such that the selected sample size will achieve a desired power for correctly detection of a prespecified clinically meaningful difference at a given level of significance. In clinical research, however, it is not uncommon to perform sample size calculation with inappropriate test statistics for wrong hypotheses regardless what study design is employed. This book provides formulas and/or procedures for determination of sample size required not only for testing equality, but also for testing non-inferiority/superiority, and equivalence (similarity) based on both untransformed (raw) data and log-transformed data under a parallel-group design or a crossover design with equal or unequal ratio of treatment allocations. It provides not only a comprehensive and unified presentation of various statistical procedures for sample size calculation that are commonly employed at various phases of clinical development, but also a well-balanced summary of current regulatory requirements, methodology for design and analysis in clinical research, and recent developments in the area of clinical development.


more






For More Information Go To the:

A set of slides with annotated examples explaining howto use the CTS, and describing its features.




.: What is the Clinical Trial Simulator (CTS)?
A free software package that can simulate Randomized Controlled Clinical Trials (RCTs). With the CTS a user can explore aspects of the design, conduction and analyses of RCTs
.: Pragmatic Randomized Controlled Trials In Health Care


This program is one of the tools been developed by PRACTIHC. Please visit the PRACTIHC website for more information.
.: How it works?
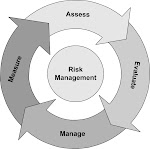
Typically, the user conceives a trial, including risk subgroups, sample size, outcome rates, effect size, lost to follow-up, compliance, stopping rules, etc. Then the program generates 1000s of such trials. A summary of the results is presented, including relative risks, relative risk reductions, confidence intervals, p-values, etc. A number of graphics is also available. The simulator also includes a sample size calculator for cluster or individually randomized trials.

.: What can be used for?
To learn how to design, analyze and report RCTs. The program tries to comply with the recommendations of the CONSORT statement when reporting the results of the trials.To answer questions like: "What if I lose 30% of the patients?", or "What if 10% of the patients do not take their study pills? What is the likely impact of these problems on the results of the study?In the current version the user can define the proportion of patients that are lost-to-follow-up, and the proportion not complying with assigned intervention, in one or more populations subgroups.Explore the impact of sample size on study results. Can be also used as a sample size calculator, taking into account the impact of lost to follow-up and protocol violations.Explore the impact on sample size of changing inclusion / exclusion criteria by changing the risk profile of study subjects.To use and teach "physiological statistics".
.: Funding
The development of this simulator was partially supported by PRACTIHC with funding from the European Commission's 5th Framework international collaboration with Developing Countries, Research Contract. ICA4-CT-2001-10019, and by the Global Health Research Initiative (GHRI) of the Canadian Institutes of Health Research (CIHR).
.: Development
The simulator was inspired on a trial simulator developed by D.W. Taylor, E.G. Bosh and D. Sacket in 1990. (D.W. Taylor, E.G. Bosch. CTS: a clinical trials simulator, Statistics in Medicine, 9:787-801,1990). [MEDLINE]
IcebergSim was designed by Eduardo Bergel and David Sackett. Eduardo Bergel is the main developer. Luz Gibbons participated in the development of the Cluster and the Stopping Rules Modules, and as a beta tester. The logo was designed by Steve Janzen.
Marcelo Delgado, Alvaro Ciganda and Martin Silva participated in the development of the previous version (v 1.0). The software was developed using the python programming language, with the qt GUI toolkit. Graphics were developed using and external, free graphic library (PLOTICUS).


more




ARTICLES
Study design in clinical research: sample size estimation and power analysis
J Lerman Department of Anaesthesia, Hospital for Sick Children, Toronto, Ontario, Canada. lerman@sickkids.on.ca
The purpose of this review is to describe the statistical methods available to determine sample size and power analysis in clinical trials. The information was obtained from standard textbooks and personal experience. Equations are provided for the calculations and suggestions are made for the use of power tables. It is concluded that sample size calculations and power analysis can be performed with the information provided and that the validity of clinical investigation would be improved by greater use of such analyses.
This article has been cited by other articles:

Y. L. Yang, H. Y. Lai, J. J. Wang, P. K. Wang, T. Y. Chen, C. C. Chu, and Y. LeeThe timing of haloperidol administration does not affect its prophylactic antiemetic efficacy: [Le moment choisi pour l'administration d'haloperidol n'affecte pas son efficacite anti-emetique prophylactique]Can J Anesth, May 1, 2008; 55(5): 270 - 275. [Abstract] [Full Text] [PDF]

Y. Lee, P. K. Wang, H. Y. Lai, Y. L. Yang, C. C. Chu, and J. J. WangHaloperidol is as effective as ondansetron for preventing postoperative nausea and vomiting: [L'haloperidol est aussi efficace que l'ondansetron dans la prevention des nausees et vomissements postoperatoires]Can J Anesth, May 1, 2007; 54(5): 349 - 354. [Abstract] [Full Text] [PDF]

Z. Xia, Z. Huang, and D. M. AnsleyLarge-Dose Propofol During Cardiopulmonary Bypass Decreases Biochemical Markers of Myocardial Injury in Coronary Surgery Patients: A Comparison with Isoflurane.Anesth. Analg., September 1, 2006; 103(3): 527 - 532. [Abstract] [Full Text] [PDF]

H. L. Mollison, W. P.S. McKay, R. H. Patel, S. Kriegler, and O. E. NegraeffReactive hyperemia increases forearm vein area: [L'hyperemie reactionnelle augmente l'aire veineuse de l'avant-bras].Can J Anesth, August 1, 2006; 53(8): 759 - 763. [Abstract] [Full Text] [PDF]

K.-S. Liu, J.-I. Tzeng, Y.-W. Chen, K.-L. Huang, C.-H. Kuei, and J.-J. WangNovel depots of buprenorphine prodrugs have a long-acting antinociceptive effect.Anesth. Analg., May 1, 2006; 102(5): 1445 - 1451. [Abstract] [Full Text] [PDF]

Y. Lee, H.-Y. Lai, P.-C. Lin, Y.-S. Lin, S.-J. Huang, and M.-H. ShyrA Dose Ranging Study of Dexamethasone for Preventing Patient-Controlled Analgesia-Related Nausea and Vomiting: A Comparison of Droperidol with SalineAnesth. Analg., April 1, 2004; 98(4): 1066 - 1071. [Abstract] [Full Text] [PDF]

J.-I. Tzeng, K.-S. Chu, S.-T. Ho, K.-I Cheng, K.-S. Liu, and J.-J. WangProphylactic iv ondansetron reduces nausea, vomiting and pruritus following epidural morphine for postoperative pain control: [L'administration prophylactique d'ondansetron iv reduit les nausees, les vomissements et le prurit qui suivent l'administration peridurale de morphine analgesique postoperatoire]Can J Anesth, December 1, 2003; 50(10): 1023 - 1026. [Abstract] [Full Text] [PDF]

P. SlingerREPLYCan J Anesth, October 1, 2003; 50(8): 864 - 864. [Full Text] [PDF]

Y. Lee, H.-Y. Lai, P.-C. Lin, S.-J. Huang, and Y.-S. LinDexamethasone prevents postoperative nausea and vomiting more effectively in women with motion sickness: [La dexamethasone previent plus efficacement les nausees et les vomissements postoperatoires chez les femmes atteintes du mal des transports]Can J Anesth, March 1, 2003; 50(3): 232 - 237. [Abstract] [Full Text] [PDF]

E. Gurses, H. Sungurtekin, E. Tomatir, C. Balci, and M. GonulluThe addition of droperidol or clonidine to epidural tramadol shortens onset time and increases duration of postoperative analgesia: [L'addition de droperidol ou de clonidine a l'administration peridurale de tramadol raccourcit le delai d'installation et prolonge la duree de l'analgesie postoperatoire]Can J Anesth, February 1, 2003; 50(2): 147 - 152. [Abstract] [Full Text] [PDF]

M. Elhakim, M. Nafie, K. Mahmoud, and A. AtefDexamethasone 8 mg in combination with ondansetron 4 mg appears to be the optimal dose for the prevention of nausea and vomiting after laparoscopic cholecystectomy : [Une dose de 8 mg de dexamethasone combinee a 4 mg d'ondansetron apparait comme la dose optimale pour prevenir les nausees et les vomissements post cholecystectomie laparoscopique]Can J Anesth, November 1, 2002; 49(9): 922 - 926. [Abstract] [Full Text] [PDF]

J.-J. Wang, S.-T. Ho, Y.-H. Uen, M.-T. Lin, K.-T. Chen, J.-C. Huang, and J.-I. TzengSmall-Dose Dexamethasone Reduces Nausea and Vomiting After Laparoscopic Cholecystectomy: A Comparison of Tropisetron with SalineAnesth. Analg., July 1, 2002; 95(1): 229 - 232. [Abstract] [Full Text] [PDF]

J.-J. Wang, J.-I. Tzeng, S.-T. Ho, J.-Y. Chen, C.-C. Chu, and E. C. SoThe Prophylactic Effect of Tropisetron on Epidural Morphine-Related Nausea and Vomiting: A Comparison of Dexamethasone with SalineAnesth. Analg., March 1, 2002; 94(3): 749 - 753. [Abstract] [Full Text] [PDF]

E. S. Aziz and M. RagehDeep topical fornix nerve block versus peribulbar block in one-step adjustable-suture horizontal strabismus surgeryBr. J. Anaesth., January 1, 2002; 88(1): 129 - 132. [Abstract] [Full Text] [PDF]

S.-T. Ho, J.-J. Wang, J.-I. Tzeng, H.-S. Liu, L.-P. Ger, and W.-J. LiawDexamethasone for Preventing Nausea and Vomiting Associated with Epidural Morphine: A Dose-Ranging StudyAnesth. Analg., March 1, 2001; 92(3): 745 - 748. [Abstract] [Full Text] [PDF]

J.-J. Wang, S.-T. Ho, C.-S. Wong, J.-I. Tzeng, H.-S. Liu, and L.-P. GerDexamethasone prophylaxis of nausea and vomiting after epidural morphine for post-Cesarean analgesiaCan J Anesth, February 1, 2001; 48(2): 185 - 190. [Abstract] [Full Text] [PDF]

J. I. Tzeng, J. J. Wang, S. T. Ho, C. S. Tang, Y. C. Liu, and S. C. LeeDexamethasone for prophylaxis of nausea and vomiting after epidural morphine for post-Caesarean section analgesia: comparison of droperidol and salineBr. J. Anaesth., December 1, 2000; 85(6): 865 - 868. [Abstract] [Full Text] [PDF]

J.-J. Wang, S.-T. Ho, S.-C. Lee, Y.-C. Liu, and C.-M. HoThe Use of Dexamethasone for Preventing Postoperative Nausea and Vomiting in Females Undergoing Thyroidectomy: A Dose-Ranging StudyAnesth. Analg., December 1, 2000; 91(6): 1404 - 1407. [Abstract] [Full Text] [PDF]

R. Zarauza, A. N. Saez-Fernandez, M. J. Iribarren, F. Carrascosa, M. Adame, I. Fidalgo, and P. MonederoA Comparative Study with Oral Nifedipine, Intravenous Nimodipine, and Magnesium Sulfate in Postoperative AnalgesiaAnesth. Analg., October 1, 2000; 91(4): 938 - 943. [Abstract] [Full Text] [PDF]

J.-J. Wang, S.-T. Ho, J.-I. Tzeng, and C.-S. TangThe Effect of Timing of Dexamethasone Administration on Its Efficacy as a Prophylactic Antiemetic for Postoperative Nausea and VomitingAnesth. Analg., July 1, 2000; 91(1): 136 - 139. [Abstract] [Full Text] [PDF]

J.-J. Wang, S.-T. Ho, Y.-H. Liu, C.-M. Ho, K. Liu, and Y.-Y. ChiaDexamethasone Decreases Epidural Morphine-Related Nausea and VomitingAnesth. Analg., July 1, 1999; 89(1): 117 - 117. [Abstract] [Full Text] [PDF]



more